One of the major subjects of discussions about the constant changes that we see in our economy is the composition of full verses part time jobs. Are most of the new jobs being created since the Great Recession part-time jobs?

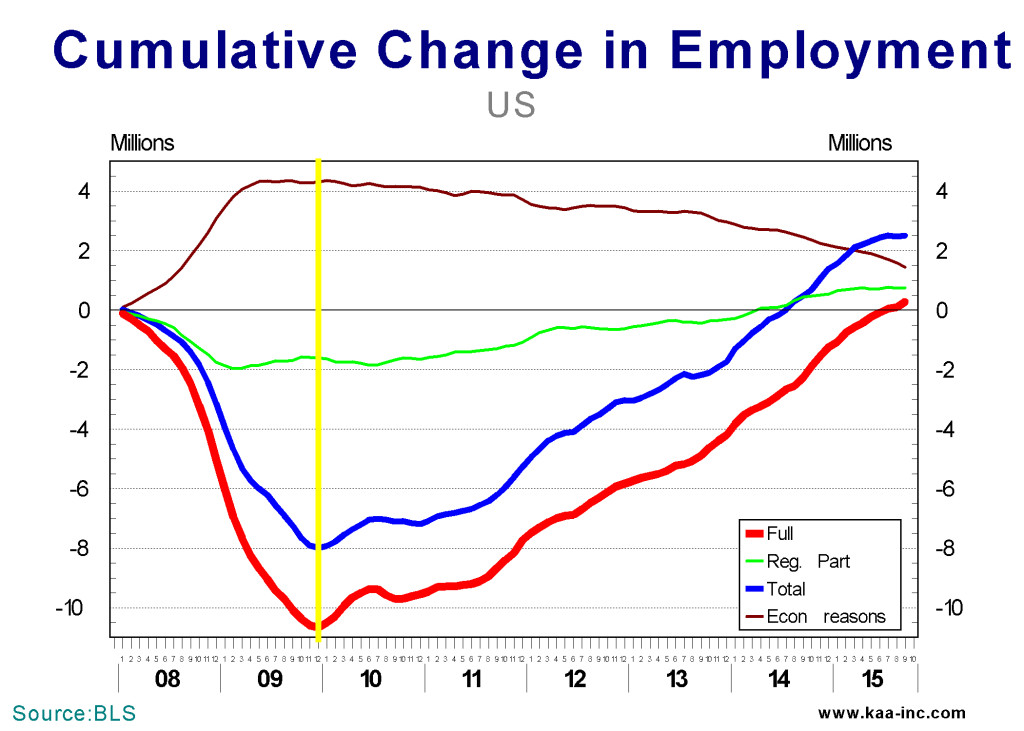
During the Great Recession we lost a disproportionate number of full-time jobs compared to previous recessions. By the end of 2009, a year into the recession, more than 11.3 million or 9.3% of all full-time jobs were lost. During the 2000-01 recession the drop in full-time jobs was 2.2 million accounting for only 2.0% of all full-time jobs. Even in the devastating double dip recession of 1980-84, the full-time job loss was 3.3 million which back then accounted for 3.9% of all the full-time jobs.

There are two types of people who hold part-time jobs, there are those who actually want a part-time job and are not looking for anything else, and then there are those who are holding part-time jobs solely due to economic reasons, that is they are looking for a full-time job but out of economic necessity have accepted a part-time job for now. These are what the Bureau of Labor Statistics labels the later group as “involuntary” part-timers. Over the last 50 years, the highest level of involuntary part-time jobs was at 37.3% which happened in 1982 during the double dip recession of the time, and lowest percentage was 13.6% which happened at the end of 1999. During the economic boom years of 2003-06 this number averaged at 18.0%. There are always people who hold part-time jobs who are looking for full time position. The distinction of this group is that while they are holding a part time job they are still looking for full time job, and as such are in actual competition with those we actually count as unemployed for a job.

During the Great Recession, the percent of involuntarily part-timers as a share of all part-timers rose to 33.8% by 2009. One out of every three part-time workers was looking for a full-time job while out of economic necessity had accepted part-time work.

The number of people who involuntarily held part-time jobs rose by 4.5 million during the 2008-09 period.

Labor market started to improve from the beginning of 2010. The number of full-time jobs started to rise along side some gains in the number of regular (voluntary) part-time jobs. Also of importance is that the number of involuntary part-time jobs started to drop. As of September 2015, the percent of involuntary part-timer dropped to 22.4%. Not yet back at around 18% which prevailed during the early 2000s, but far for the more than 33% which prevailed in March 2009.

The total number of jobs created since December 2009 is 10.8 million. Since we lost 8.6 million jobs during the Great Recession, the economy is now 2.2 million jobs ahead of where it was in 2007. This however, does not tell the whole story, in the sense that it combines part and full-time jobs. To get a more accurate look at this, we need to dissect the data to its proper components.

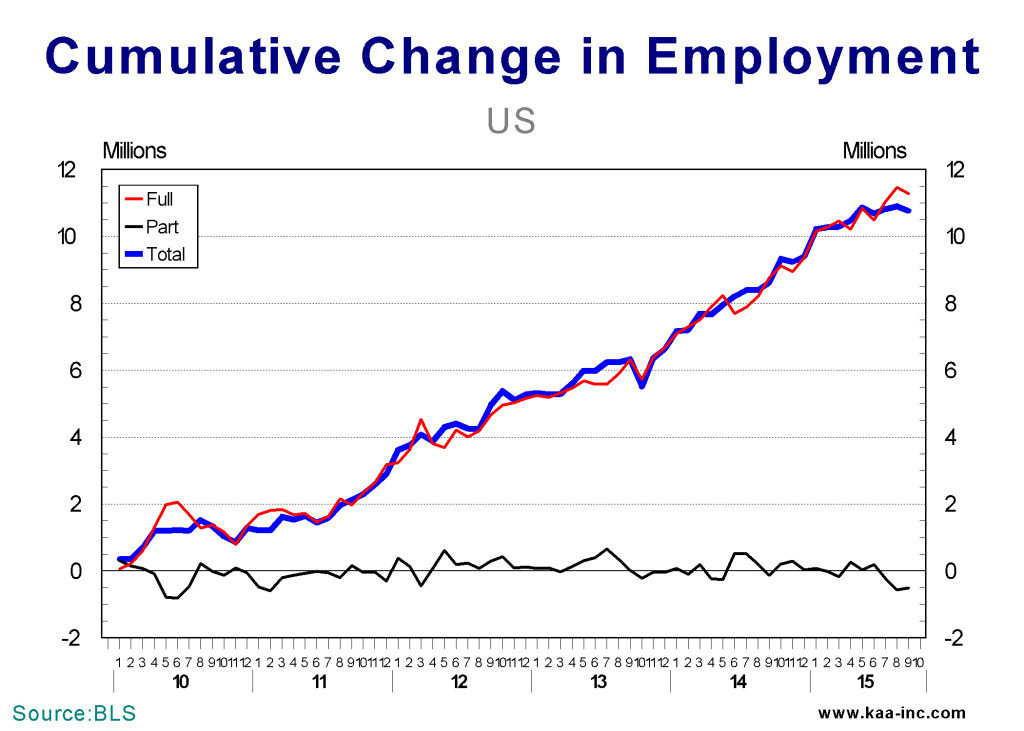
The total number of full-time jobs created since December 2009 is 11.3 million. Considering that during the Great Recession we lost 11.3 million full-time jobs, we are just back where in November 2007.

Part-time jobs reacted differently to the recession, while the number involuntary part-time worker zoomed up to 4.5 million, the number of those who regularly held part-time jobs collapsed by more than 2 million during the recession. Between December 2009 and September 2015, the total number of part-time jobs has dropped by 0.5 million. This doesn’t mean that no new part-time jobs were created since 2009, actually 2.5 million new regular part-time jobs were created, however, almost 3 million part-time jobs held involuntarily have gone away resulting in a net loss of 0.5 million in total part-time jobs.

Between December 2009 and September 2015, the economy created 11.3 million full time and close to 3 million regular part time jobs. This puts the number of jobs added at 14.3 million. Accordingly, 79% of all the new jobs created after the recession are full-time jobs. During the same period 3.5 million involuntary part-time jobs were lost or converted to full time. Subtracting the jobs lost form those added gives us a net gain of 10.8 million jobs since December 2009.

The job market continues to expand at a healthy rate, and the ratio of full time to part time jobs is holding relatively constant. Over the last 12 months, 8 out of every 10 jobs created were full time Jobs. Accordingly the notion that most of the jobs that are being created are part-time jobs, is grossly inaccurate.